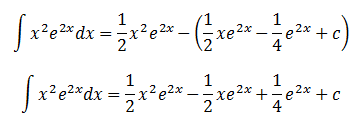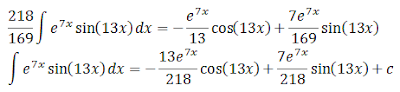Born: Frobenius

Ferdinand Georg Frobenius was born this day in 1849. If you did not enjoy finding series solutions around a singular point (Section 5.4, 5.5 & 5.6), you should blame him. It's his fault.

RIP Euler

Leonard Euler died this day in 1783.

He was a good guy.

Calc 2 Review: Partial Fractions

Introduction
To begin with, we'll return to the wonderful world of arithmetic. If we wanted to add to fractions, it is just a matter of finding a common denominator.

If we started with 31/35 and wanted to go back to two separate terms summed from 5th and 7th, how would we go about doing so?

To make our lives more simple, we will multiply by the least common denominator to clear the fractions and end up with 31 = 7A +5B. In this example, we get an underdetermined system of equations (two unknowns but only one equation). In fact there are an infinite number of A’s and B’s that would. We know that A=3 and B=2 works, but so does A = 8 and B= -5. Luckily, when dealing with polynomials, we get no such complications. If P(x) is a factorable polynomial, then the rational expression Q(x)/P(x) can be rewritten as the sum of polynomials with the denominators from the factors of P(x). That was a lot of math talk, let’s get into the examples.

Example One

We can factor the denominator and set up our equation like so

Multiplying both sides by the LCD we get:

1=A(x+1) +B(x-1) or 1= (A+B)x + (A-B)

Our goal is to solve for A and B. The first method is to match up the coefficients on the powers of x. On the right hand side we have 0 = A + B for the x term (or more specifically, “x to the one power” term) and 1 = A – B for the constant term (“x to the zero power”)

With two equations, we can solve the system using substitution, graphing, elimination, Gauss-Jordan elimination, Cramer’s Rule (and probably some other methods, too).

No matter how you do it, you end up with A = 1/2 B = -1/2.

So, 

If you want to double check your work using a technological aid, you can graph both equations on your calculator. As long as you are careful with your parenthesis, the graph of y1= 1/(x^2 – 1) and y2=(1/2)(1/(x-1)-1/(x+1) should come out the same.

Example Two

In this case, when we factor the denominator, we get a repeated factor. The rules for partial fractions tell us that we have to include each power of each factor. So we will start off with

Multiplying by the LCD gives us (x+3)=A(x+2)+B
We could solve for A and B by matching up the coefficients. Instead, we use will use a slightly different method. The equation has to be true for any value of x, so we will just pick strategic values of x. If x = -2, then the equation simplified down to 1 = 0 + B, so B = 1. Knowing this, we choose x = 0 and get the equation 3 = 2A + B. We know B = 1. Substituting and solving we get A = 1.

Example Three

When we factor the denominator, we get an irreducible/un-factorable quadratic. That’s ok. In this case, we set up the partial fraction like so:

Please note the numeration in the second term. Because we have an irreducible quadratic in the denominator, we have to have a linear term up top. 
To solve the problem, we follow the same process of multiplying by the least common denominator and solving for A, B, and C from there.

Rather than foil out the second term, I am going to pick values for x and build my equations that way. 
When x =-1, 9 = 2A
When x = 0, 8 = A + C
When x = 1, 9  = 2A + 2B + 2C
Back substituting, the numbers get a little bit ugly. We end up with 

Summary

Partial fractions only work with rational expressions. That is a polynomial divided by a polynomial. Also, they need to be proper fractions.If the degree of the numerator is the same or larger than the the degree of the denominator, first do polynomial long division and then use partial fractions on the remainder.
The most common mistake is initially setting up the fraction wrong. Remember the rules for linear factors (Example 1), repeated factors (Example 2) and quadratic factors (Example 3). The second most common mistake is to make an arithmetic error, so take your time and try to check your work.

That is the basics of partial fractions. They are not going away. Get good at partial fractions; they're coming back in Chapter 6 (and possibly before then, too).

Calc 2 Review: Integration By Parts

LEVEL 1: Basic Integration by parts

This is the most basic integration by parts problem that there is. In this case, the hardest part is not messing up the sign after during the trig integration.

LEVEL 2: Integration by parts, the sequel

Doing integration by parts once does not get us to answer. We have to do integration by parts on the second term of the right-hand-side.

 Substituting back into the first time we did integration by parts, we get:

We finally get an answer.

We could have sped up the process by using the Tabular Method.

LEVEL 3: The neverending integration by parts.

Step One: Swear. (This step is Optional)
Step Two: Remember back to Algebra I.
   Given the equation:   a = b – 4a     Solve for a
   That’s easy. Add 4a to both sides, get 5a = b
   Divide both sides by 5, get a = b/5
   Piece of Cake.

Step Three: After reminiscing, return to the problem at hand and try integration by parts, twice.

Step Four: Remember that side trip we took back at Step Two. Our equation right now looks something like:

We are trying to solve for the integral. It's the same form as a = b - 4a

In this case, a is the integral, b has two ugly terms and instead of having 4 as a coefficient on a we have a coefficient of 49/169. We solve it the same way that we did the Algebra I problem.

Don't forget to add the + c. It would be a pity to do all the hard work and lose a point because of the + c.

SUMMARY

When using integration by parts on the repeating functions (Like the "Level 3" problem), you should only have to do integration by parts twice. If you find that you have done integration by parts three or four times, you are likely headed in the wrong direction.

LIATE is the rule of thumb for doing integration by parts. When trying to pick which term to differentiate (what the u is). Usually Pick in this order:
L - Logarithmic functions: ln(x)
I - Inverse trig functions: arcsin(x)
A - Algebraic functions: (i.e. polynomials)
T - Trig functions: sin(x)
E - Exponential functions: e^x

You should be able to do any similar problems (Level 1, 2 or 3) by the time the first exam comes around. Integration by parts will return in Section 3.6 and Section 4.4, so you want to master this skill.

Online Resources Part 1

There are some online resources that might be useful to students in Diff Eq.

DField 2005.10.
DField will graph Direction/Slope Fields, something that your calculator might not do. Here is what the interface looks like.

click on the image to enlarge

The application runs using Java and will pop-up as three different windows. The Message window, pictured top-left, is not particularly useful and can probably be ignored. The Equation window, pictured bottom-left, is where you enter the differential equation. The program uses variables in a slightly unconventional way. Instead of using x and y, the program uses x as the dependent variable (where we normally use y) and t as the independent variable (where we would normally use x). In the example, I graphed the slope field for x'=2t. In the Direction Field window, pictured right, gives a picture of the direction/slope field for whatever equation you have entered.

Having passed Calc 2, we know that the general solution to x'=2t should be a parabola. By clicking anywhere on in the direction field, it will give you a particular solution (Those are the blue parabolas in the picture). If I click on the "Solutions" Tab and then "Keyboard Input of Initial Value" under that menu, a fourth window will pop up giving you the option of directly entering an initial value for t and x.

DField will be useful early on, when we are working on solving first-order differential equations. It may also help when we look at autonomous equations. It's value will fade as the semester goes on.

Online Videos at Khan Academy or via iTunes U.

Khan Academy offers short videos for both calculus and Diff Eq. The calculus videos might be helpful if you want to review subjects from Calc 2. If you are not completely confident in your ability to solve a problem involving Integration by Parts or Partial Fractions Decomposition, you need to become so. Those types of problems are not going away.

For the iCrowd, iTunes U is one of the tabs in the iTunes Store. You can download specific lectures and watch them in places where you can't stream video from Khan Academy. While Khan Academy videos tend to be short and specific to one topic, the videos on iTunes U tend to look more like a traditional classroom lecture.

Also, if you just look on YouTube, you can usually find some math help there, too. Just don't get distracted by Epic Rap Battles of History or the other awesome stuff on YouTube.

The ASC at Orchard Ridge.

The Academic Skills Center over in K-Building offers free tutoring by appointment. Just click on the "OR ASC Tutor Schedule" to see what is available. Appointments are made over the phone or in-person in K-100. Appointments can made for 1-hour, twice a week (depending on availability). The number of math tutors available to help with Diff Eq tends to be small. To overcome this, there are a few things you can try. First off, be ahead of the game. You can schedule appointments up to two weeks in advance. Secondly, do not get behind elsewhere. The ASC offers lots of tutors for classes other than math. Going and visiting one of the fabulous physics tutors or lovely chemistry tutors might help you stay ahead in those classes and thereby give you more time to work on Diff Eq.

Email the Instructor.

If you e-mail Prof. Reynolds, she is really good about getting back to you.

Comment on the Blog.

Feel free to post questions or comments on the Blog. If you drop me an e-mail or send me a message on Facebook, I'll probably will never get back to you. I rarely check my OCC e-mail and I avoid going on Facebook as much as possible.

We Few, We Happy Few

He that outlives this day, and comes safe home,
Will stand a tip-toe when the day is named,
And rouse him at the name of Crispian.
He that shall live this day, and see old age,
Will yearly on the vigil feast his neighbours,
And say 'To-morrow is Saint Crispian:'
Then will he strip his sleeve and show his scars.
And say 'These wounds I had on Crispin's day.'
Old men forget: yet all shall be forgot,
But he'll remember with advantages
What feats he did that day: then shall our names.
Familiar in his mouth as household words
Harry the king, Bedford and Exeter,
Warwick and Talbot, Salisbury and Gloucester,
Be in their flowing cups freshly remember'd.
This story shall the good man teach his son;
And Crispin Crispian shall ne'er go by,
From this day to the ending of the world,
But we in it shall be remember'd;
We few, we happy few, we band of brothers;
For he to-day that sheds his blood with me
Shall be my brother; be he ne'er so vile,
This day shall gentle his condition:
And gentlemen in England now a-bed
Shall think themselves accursed they were not here,
And hold their manhoods cheap whiles any speaks
That fought with us upon Saint Crispin's day.

Henry V, Act 4, Scene 3